- 深層学習を勉強しようと思って,深層学習の本[1]を読んだ.
- さらに,MNISTデータセット[2]を使って,手書き数字認識プログラムを作った
- MNISTは,分類器を作る時のHello worldみたいなの
- 一番簡単な順伝播型ニューラルネットワーク(FFNN)を使う(他はよくわからん)
- 1章から4章あたりまで読めば実装に必要な情報が揃う
- 入力層,中間層,出力層の3層だけで構成
- 行列計算,データセットは既存のパッケージを使う
- 画像認識プログラムそれ自体は自分で実装する(caffe,TensorFlow等を使わない)
- この界隈ではPythonがスタンダードらしいので,それに従う
- ただ,Jupyter(IPython)は準備がめんどくさかったので保留
- ソースコードは全部まとめて[3]に置いておく
順伝播型ニューラルネットワークの構築
-
構造が簡単な順伝播型ニューラルネットワーク(FFNN)を採用
- 多層パーセプトロンともいう
-
入力データを,多クラスに分類させる
-
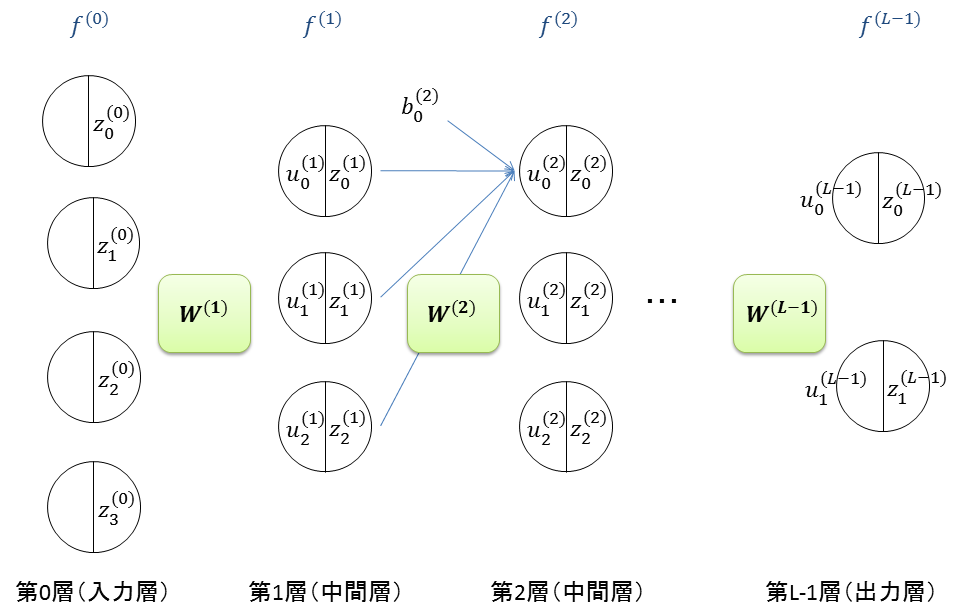
ネットワークは図のように構築する
- \(L\): 層の数.入力層,中間層,出力層の3層があればよい
- \(f^{(l)}(u)\): 第\(l\)層における活性化関数
- \(f^{(l)}(u) = \frac{1}{1+e^{-u}} \): 出力層以外なら,ロジスティック関数を使う
- \(u_i^{(l)}\): 第\(l\)層の\(i\)番目のユニットにおける入力
- \(z_{i}^{(l)}=f^{(l)}(u_i^{(l)})\): 第\(l\)層の\(i\)番目のユニットにおける出力
- \(\mathbf{W}^{(l)}\): 第\(l-1\)層と第\(l\)層の間の重みを要素にもつ行列
-
各層の入出力を列ベクトルで表す
- \(\mathbf{u^{(l)}} = [u_0^{(l)} u_1^{(l)} \dots u_i^{(l)} \dots]^{T}\): 第\(l\)層のユニットへの入力を表す列ベクトル
- \(\mathbf{z^{(l)}} = [z_0^{(l)} z_1^{(l)} \dots z_i^{(l)} \dots]^{T}\): 第\(l\)層のユニットの出力を表す列ベクトル
-
この時,順方向(入力層->中間層->出力層)の伝播は以下のように行列演算で書ける
- 入力を列ベクトル\(\mathbf{x}\)とすると,\(\mathbf{z}^{(0)} = \mathbf{x}\)
- 出力を列ベクトル\(\mathbf{y}\)とすると,\(\mathbf{y} = \mathbf{z}^{(L-1)}\)
- \(\mathbf{u^{(l+1)}} = \mathbf{W}^{(l+1)} \mathbf{z}^{(l)} + \mathbf{b}^{(l+1)}\)
- \(\mathbf{z^{(l+1)}} = f^{(l+1)}(\mathbf{u^{(l+1)}})\)
- ただし,\(\mathbf{b}^{(l)}\)は第\(l\)層のバイアス
-
分類するだけならここで終わり.\(\mathbf{y}\)が分類結果.
-
学習段階であれば,次に逆方向(出力層->中間層->入力層)の伝播を行う.
- \(\mathbf{d}\): \(\mathbf{x}\)の正解データ
- \(\mathbf{\Delta}^{(L-1)} = \mathbf{z}^{(L-1)} - \mathbf{d}\)
- \(\mathbf{\Delta}^{(l)} = f^{(l)’} ( \mathbf{u^{(l)}} ) \odot \mathbf{W}^{(l+1)T} \mathbf{\Delta}^{(l+1)} \)
- \(\odot\): 行列の要素同士の積
- \(f^{(l)’}(u)\): \(f^{(l)}(u)\)の導関数
-
\(\mathbf{\Delta}^{(l)}\)が求まれば,それをもとに重みとバイアスを更新する.
- \(\mathbf{W}^{(l)} \leftarrow \mathbf{W}^{(l)} - \epsilon \mathbf{\Delta^{(l)}} \mathbf{z}^{(l-1)T} \)
- \(\mathbf{b}^{(l)} \leftarrow \mathbf{b}^{(l)} - \epsilon \mathbf{\Delta^{(l)}} [1 1 \dots 1]^T \)
- \(\epsilon\): 学習係数.
-
学習係数,重みの初期値,ユニット数,学習回数の決定は経験則なのかな
-
複数の訓練データ(ミニバッチ)を同時に流すと並列化の効率が良いらしいので,下のプログラムではミニバッチを使うようにしている
# 行列の各要素にlogistic()を適用
def logistic(U):
return 1.0/(1.0 + np.exp(-1.0*U))
# 行列の各要素にlogistic_deriv()を適用
def logistic_deriv(U):
t = logistic(U)
return t * (1.0-t)
def softmax(U):
U = U - np.max(U, axis=0) # Uを正規化
U = np.exp(U) # 全要素にexp()を適用
U = U / np.sum(U, axis=0)
return U
# 多層ネットワーク, 多クラス分類器
class FeedforwardNeuralNetwork:
# コンストラクタ
# sizes: 入力層,中間層,出力層のユニット数
# f: 活性化関数.ただし,入力層では不要
# f_deriv: 中間層のみ
def __init__(self, sizes, f, f_deriv):
# 各層のユニット数
self.sizes = sizes
# 層の数
self.L = len(sizes)
# 活性化関数f,活性化関数の導関数f_deriv
self.f, self.f_deriv = f, f_deriv
# 各層の重みW,バイアスb
self.W, self.b = list(range(self.L)), list(range(self.L))
for l in range(1,self.L):
self.W[l] = np.random.uniform(-1.0,1.0,(sizes[l], sizes[l-1]))
self.b[l] = np.random.uniform(-1.0,1.0,(sizes[l], 1))
# ネットワークにデータを伝搬させる
#
# X=[x1,x2,...xn]: 入力データ(ミニバッチ),各データxiは列ベクトル
# D=[y1,y2....yn]: Xに対応する正解出力
#
# D==[]: 順伝播により推測する.返値は,Xに対応する出力.
# D!=[]: 順伝播と逆伝播により重みを学習する.返値は,誤差.
def propagate(self, X, D = []):
# --- 順伝播 ---
N = len(X[0]) # 列数
Z, U = list(range(self.L)), list(range(self.L))
Z[0] = np.array(X,dtype=np.float64)
for l in range(1,self.L):
U[l] = np.dot(self.W[l],Z[l-1]) + np.dot(self.b[l],np.ones((1,N)))
U[l] = U[l].astype(np.float64)
Z[l] = self.f[l]( U[l] )
if len(D)==0:
return Z[self.L-1]
# --- 逆伝播 date: 2016-04-24T00:00:00-00:00
draft: false
---
De = list(range(self.L))
Y = Z[ self.L -1]
D = np.array(D)
eps = 0.4 # 学習係数
# De の計算
De[ self.L-1 ] = Y - D # 注意.P51とは違う.P49を見るとこちらが正しい?
for l in range(self.L-2,0,-1):
De[l] = self.f_deriv[l]( U[l] ) * np.dot(self.W[l+1].T , De[l+1] )
# W,bの更新
for l in range(self.L-1,0,-1):
self.W[l] = self.W[l] - eps/N*np.dot(De[l] , Z[l-1].T)
self.b[l] = self.b[l] - eps/N*np.dot(De[l] , np.ones((N, 1)))
# 誤差を返す
return np.power(De[self.L-1],2).sum()/N
動作確認
- 2進数3ケタから10進数1ケタへの変換を先ほどのネットワークにやらせてみる
- 110 -> 6みたいなの
# リストliの中で最も大きな数値に対応するindexを返す
# l2n( [00 11 27 19 18] ) -> 2
def l2n(li):
return max(range(len(li)), key=(lambda i: li[i]))
# 数値xをサイズ10のリストに変換する
# n2l(3) -> [0 0 0 1 0 0 0 0 0 0]
def n2l(x):
res = [0,0,0,0,0,0,0,0,0,0]
res[x] = 1
return res
# 2進から10進への変換によるFeedforwardNeuralNetworkの動作確認
def binary2decimal_test():
dl = FeedforwardNeuralNetwork(
[3,8,10], [None,logistic,softmax], [None,logistic_deriv,None])
for i in range(1000):
dl.propagate(
[[0,1,0,1,0,1,0,1], # 訓練データ(入力)
[0,0,1,1,0,0,1,1],
[0,0,0,0,1,1,1,1]],
[[1,0,0,0,0,0,0,0], # 訓練データ(正解)
[0,1,0,0,0,0,0,0],
[0,0,1,0,0,0,0,0],
[0,0,0,1,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,1,0],
[0,0,0,0,0,0,0,1],
[0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0]])
X = [[0], # テストデータ
[1],
[1]]
Y = dl.propagate(X)
print("input:")
for i in range(2,-1,-1):
print(X[i][0], end='')
print("\nanswer:")
for i in range(10):
print(str(i) + ": " + str(int(Y[i][0]*100)) + "%")
binary2decimal_test()
- 出力結果を下に示す.
- 2進数の110が,10進数の6であると,推測できている.
input:
110
answer:
0: 0%
1: 0%
2: 1%
3: 0%
4: 1%
5: 0%
6: 95%
7: 1%
8: 0%
9: 0%
MNIST画像の識別
- MNISTは,数字を手書きした1画像あたり28x28ピクセル,70000画像のデータセット
- PythonにはMNISTデータを自動で取ってくるfetch_mldataてのがある.便利.
- 画像データは全部で70000個あって,63000個を訓練データ,7000個をテストデータとする
- データは予め0.0から1.0の範囲で正規化
- 学習係数は0.4(適当にパラメータスイープで決めた)
- 重みの初期値[-1 1]で一様乱数
- ユニット数は入力層,中間層,出力層で,それぞれ28x28,100,10(適当にパラメータスイープで決めた)
# MNISTの識別器
class MNIST:
# コンストラクタ
def __init__(self):
# MNISTデータセット
mnist = fetch_mldata('MNIST original', data_home=".")
# 画像データX,正解データy
X = mnist.data
y = mnist.target
# 0.0から1.0に正規化
X = X.astype(np.float64)
X /= X.max()
# Xとyを訓練データおよびテストデータに分割
# test_size: テストデータの割合
self.X_train,self.X_test,self.y_train,self.y_test=train_test_split(X,y,test_size=0.1)
# ネットワークを構築
self.dl = FeedforwardNeuralNetwork([28*28,100,10],
[None,logistic,softmax], [None,logistic_deriv,None])
# ネットワークを学習させる
# num: 学習回数
def learn(self, num):
# 訓練データのindex集合
train_indexes = list(range(0, self.X_train.shape[0]))
for k in range(num):
# ミニバッチ(学習の単位)を選択
minibatch = np.random.choice(train_indexes, 50)
# 訓練データ,正解データをミニバッチに合わせて抽出
inputs = []
outputs = []
for ix in minibatch:
inputs.append(self.X_train[ix])
outputs.append(n2l(int(self.y_train[ix])))
inputs = np.array(inputs).T
outputs = np.array(outputs).T
# 学習
self.dl.propagate(inputs, outputs)
# 進捗状況を出力
if k% (num//100) ==0:
if (k*100//num) % 10 ==0:
sys.stdout.write(str(k*100//num))
else:
sys.stdout.write(".")
sys.stdout.flush()
print()
# 添字ixのデータをクラス分類
# ix: テストデータ中の添字
def predict_one(self, ix):
# 多クラス分類を実行
inputs = np.array([self.X_test[ix]]).T
self.dl.propagate(inputs)
# 分類器の結果を出力
print("answer:")
for i in range(10):
print(str(i) + ": " + str(int(t[i][0]*100)) + "%")
# 画像を出力
self.show_image(self.X_test[ix])
# 全てのテストデータをテストし,精度・再現率・F値を出力
def predict_all(self):
# 多クラス分類を実行
predictions = self.dl.propagate(np.array(self.X_test).T)
# 整形
predictions = np.array(list(map(l2n, predictions.T)))
# 精度・再現率・F値を出力
print(classification_report(self.y_test, predictions))
a = MNIST()
print("start learning")
a.learn(2000)
print("start testing")
a.predict_all()
- 結果は以下のとおり
- 精度,再現率,F値はそれぞれ93%
- 手探り状態で作った割には,なかなかいい精度?
- 絶対的にはどうなのか不明
$ python3 main.py
start learning
0.........10.........20.........30.........40.........50.........60.........70.........80.........90.........
start testing
precision recall f1-score support
0.0 0.96 0.97 0.96 682
1.0 0.95 0.98 0.97 740
2.0 0.94 0.88 0.91 721
3.0 0.93 0.93 0.93 706
4.0 0.92 0.93 0.92 720
5.0 0.93 0.90 0.91 627
6.0 0.93 0.95 0.94 680
7.0 0.93 0.93 0.93 712
8.0 0.88 0.93 0.91 702
9.0 0.93 0.88 0.90 710
avg / total 0.93 0.93 0.93 7000

今後
以下のトピックを見ていく.
- 自己符号化:出力を入力に近づけるように教師なし学習で重みを更新してく
- 畳込みニューラルネットワーク(CNN): 画像処理でメジャー
- 再帰型ニューラルネットワーク(RNN):音声認識や手書き文字認識でメジャー
- ボルツマンマシン:確率的に動作(よくわからん)
参考文献
- [1] 岡谷貴之, 深層学習 (機械学習プロフェッショナルシリーズ), http://goo.gl/c0MV0f
- [2] THE MNIST DATABASEof handwritten digits, http://yann.lecun.com/exdb/mnist/
- [3] https://github.com/bobuhiro11/ffnn/blob/master/main.py