- 簡単のため1次元の波で考える
- 時刻\(t\)における座標 \(x\) の値を \(f(x-ut)\) とする
- 例えば,正弦波が速度\(u\)でx軸正方向に進むなら,\(f(x-ut) = sin(x-ut)\)
- この時,\(\frac{\partial f}{\partial t} + u \frac{\partial f}{\partial x} =0 \)が成り立つ.これが移流方程式
1次風上差分法#
- 直線で近似する
- 数値解析なので,\(x\)は\(\dots,x_{i-1},x_i,x_{i+1},\dots\)のように離散的
- \(x = x_i\)における\(f\)の近似を\(F_i^n(x)\)とする
- この手法は直線で近似するので,\(F_i^n(x)=a(x-x_i) + f_i^n, a = \frac{f_i^n - f_{i-1}^n}{\Delta x}\)
- ただし,\(f_i^n\)は\(x = x_i\)において時間ステップを\(n\)回進めた時の値
- 1時間ステップあたり時間は\(\Delta t\)だけ進む
- 時間ステップを進めると,$f_i^{n+1} = F_i^n(x_i-u\Delta t) = a(-u \Delta t) + f_i^n= - \frac{u \Delta t}{\Delta x}(f_i^n - f_{i-1}^n) + f_i^n$
- プログラムでは,$K=u \frac{\Delta t}{\Delta x}$として以下を繰り返すだけ
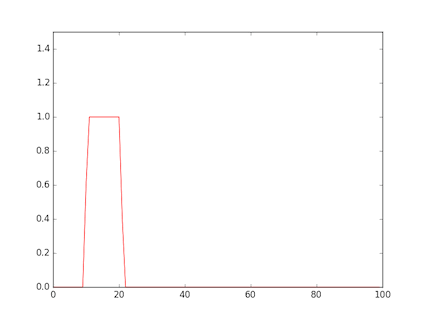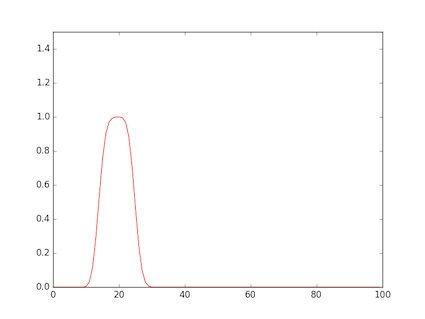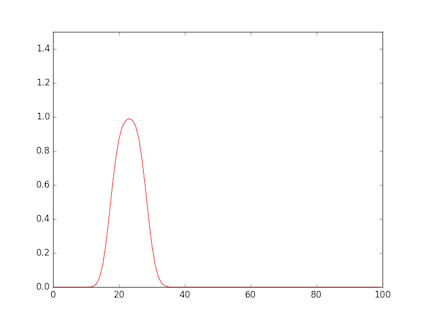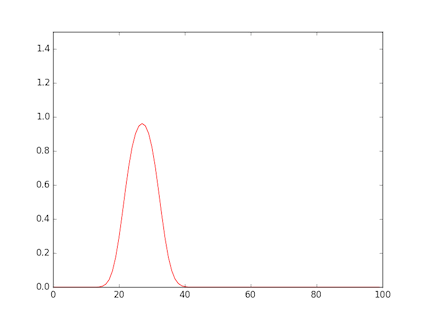
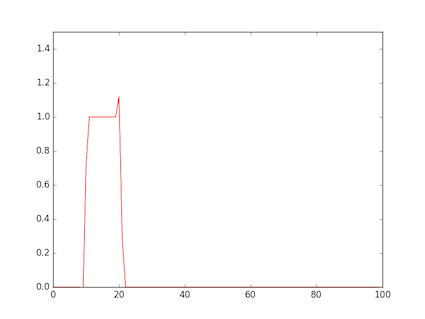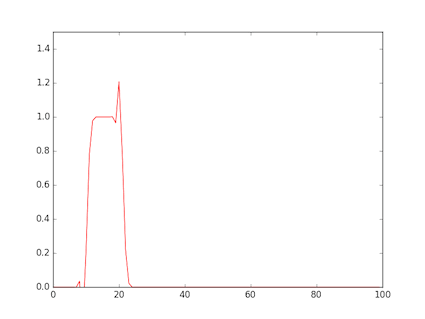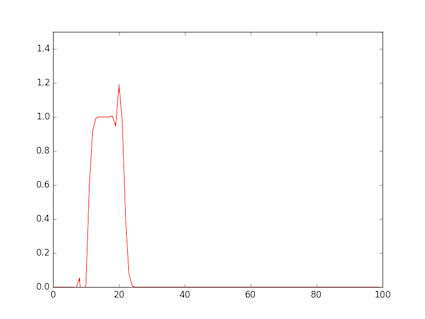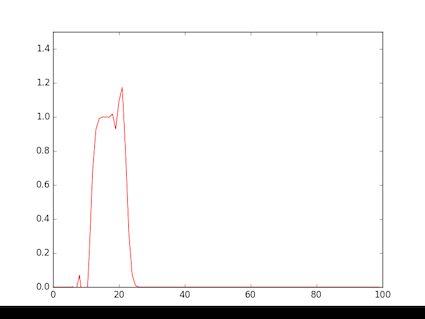
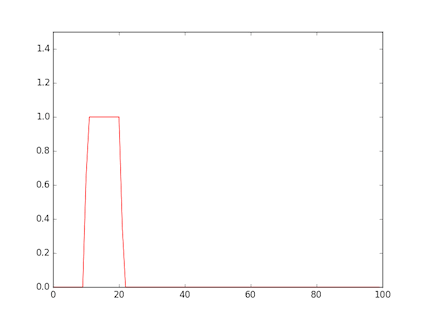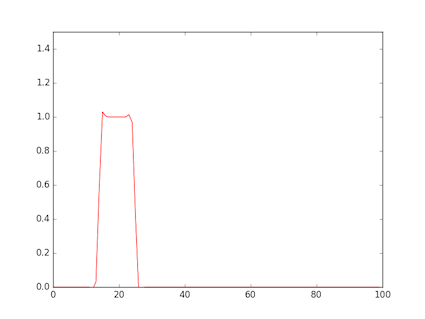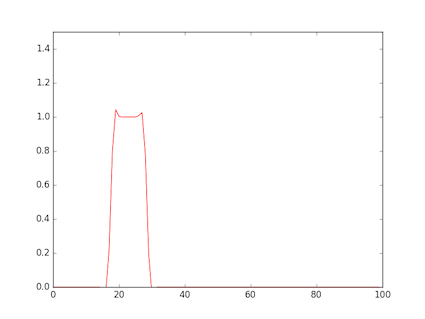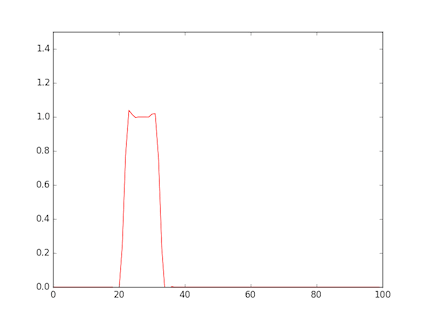
- 図は,矩形波を与えたもの
- 風下もある
for(i=1; i<99; i++) f_new[i] = -K * (f[i]-f[i-1]) + f[i];
for(i=1; i<99; i++) f[i] = f_new[i];
Lax Wendroff法#
- 二次関数で近似する
- $F_i^n(x) = a(x-x_i)^2 + b(x-x_i) + c$で近似する
- $a,b,c$3つの定数が必要なので,$x$に適当に値を入れて,
- $F_i^n(x_{i-1}) = a \Delta x ^2 - b \Delta x + c = f_{i-1}^n$
- $F_i^n(x_{i}) = c = f_{i-1}^n$
- $F_i^n(x_{i+1}) = a \Delta x ^2 + b \Delta x + c = f_{i+1}^n$
- ただし,$x_{i+1} - x_{i} = x_{i} - x_{i-1}=\Delta x$
- これを解いて,
$$
F_{i}^n(x) = a(x-x_i)^2 + b(x-x_i) + f_i^n, \\
a = \frac{f_{i+1}^n - 2f_{i}^n + f_{i-1}^n}{2\Delta x^2},
b = \frac{f_{i+1}^n - f_{i-1}^n}{2\Delta x}
$$
- 時間ステップを進めると,
$$
f_i^{n+1} = F_i^n(x_i-u\Delta t) = f_i^n - \frac{u\Delta t}{2 \Delta x}(f_{i+1}^n - f_{i-1}^n) + \frac{(u\Delta t)^2}{2 \Delta x ^2}(f_{i+1}^n -2 f_i^n- f_{i-1}^n)
$$
- プログラムでは,風上差分と同様に$K=u \frac{\Delta t}{\Delta x}$として以下を繰り返すだけ
for(i=1; i<99; i++) f_new[i] = f[i] - K*K*(f[i+1]-f[i-1])/2.0 + K*K*(f[i+1]-2*f[i]+f[i-1])/2.0;
for(i=1; i<99; i++) f[i] = f_new[i];
CIP法#
- 関数自身に加え,その微分も移流させ,3次関数で近似
- まず,移流方程式$\frac{\partial f}{\partial t} + u \frac{\partial f}{\partial x} = 0$を$x$で微分する
- $\frac{\partial g}{\partial t} + u \frac{\partial g}{\partial x} = -g \frac{\partial u}{\partial x}$
- 次に$f$を$F_i^n(x) = a(x-x_i)^3 + b(x-x_i)^2 c(x-x_i) + d$で近似する
- $F_i^n(x)$も$x$で微分しておくと,
- $\frac{d F_i^n(x)}{dx} = 3a(x-x_i)^2 + 2b(x-x_i) + c$
- $a,b,c,d$4つの定数を適当に求めていく.
- $F_i^n(x_i) = d = f_i^n$
- $\frac{d F_i^n(x_i)}{dx} = c = g_i^n$
- $F_i^n(x_{i-1}) = -a \Delta x^3+b \Delta x^2 - c \Delta x + d = f_{i-1}^n$
- $\frac{d F_i^n(x_{i-1})}{dx} = 3a \Delta x^2 - 2b \Delta x + c = g_{i-1}^n$
- これを解いて
$$
a = \frac{g_i^n + g_{i-1}^n}{\Delta x^2} - \frac{2 (f_i^n - f_{i-1}^n)}{\Delta x^3},
b = \frac{3(f_{i-1}^n + f_{i}^n)}{\Delta x^2} - \frac{2 g_i^n + g_{i-1}^n }{\Delta x} \\
$$
- 時間ステップを進めると,
$$
f_i^{n+1} = F_i^n(x_i-u\Delta t) = -a u^3 \Delta t^3 + b u^2 \Delta t ^2 -c u \Delta t + d, \\
g_i^{n+1} = \frac{F_i^n}{dx}(x_i-u\Delta t) = 3a (-u \Delta t)^2 + 2b(-u \Delta t) +c
$$
dx = 1.0; // dx
d = -dx; // -dx
gzi = -dx * K; // -dx * u * dt/dx = -u*dt
for(i=1; i<99; i++){
a = (g[i] + g[i-1]) / (d*d) + 2.0 * (f[i]-f[i-1])/(d*d*d);
b = 3.0 * (f[i-1]-f[i])/(d*d) - (2.0*g[i]+g[i-1])/d;
f_new[i] = ((a*gzi+b)*gzi+g[i])*gzi+f[i];
g_new[i] = (3.0*a*gzi+2.0*b)*gzi++g[i];
}
for(i=1; i<99; i++){
f[i] = f_new[i];
g[i] = g_new[i];
}
参考文献#


