もしも $n \ge 4$ かつ $m \ge 4$ の場合には、どうやっても条件A(縦横の長さがともに偶数の正方形内に含まれる1の数が奇数)を満たすことができない。 例えば、$2 \times 2$の正方形が条件Aを満たすとき、その正方形を4つ連結すると、 その和は偶数になってしまう。つまり、$4 \times 4$の正方形では条件Aを満たすことができない。

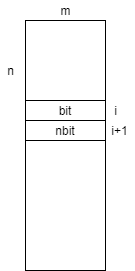
それ以外の場合には、何度か操作することで必ず条件Aを満たすことができる。 最小の操作回数はDPを使って解くことができる。 $dp_{i,bit}$を、$i$番目の行まで見たときに、$i$番目のビット列が$bit$であるときの 最小の操作回数とする。 更新式は以下の通り。ただし、$bit$と$nbit$と間で条件Aを満たすことを確認する。
$$ \begin{aligned} dp_{i+1,nbit} \Leftarrow dp_{i, bit} + \sum_{j=0}^{m-1} ((nbit » j) \& 1) \oplus a_{i+1,j} \end{aligned} $$