赤diffだった。問題文を読むと手を付けれそうな気がしたけど、そんなに簡単じゃなかった。 まず、$O(N^3)$のDPを考えて、それをもとに計算量を削減していくというアプローチを取る。
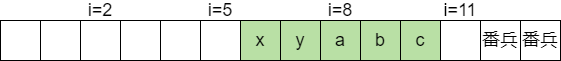
$i = 2, 5, 8, 11, \dots$ のように3文字おきに見ていく。
dp[i][x][y]を$i$番目まで見たとき、直前の2つの文字が$x$、$y$であるときの最大スコアとする。
a = v[i], b = v[i+1], c = v[i+2] として、パターン分けしていく。
スコア +1となる場合。どの3つでスコアを増やすか考える。
A) $a = b = c$ の場合、すべての$(x, y)$の組について dp[i+3][x][y] <= dp[x][y] となるので、代わりに答えに+1しておく。$O(1)$
B) $a = b = x$の場合、すべての$y$について dp[i+3][c][y] <= max(dp[i][a][*]) + 1 とする。$O(N)$
C) $a = x = y$の場合、dp[i+3][b][c] <= dp[i][a][a] + 1とする。$O(N)$
スコア +1とならない場合。どの2つを残すか考える。
D) $x$、$y$ を残す場合、dp[i+3][x][y] <= dp[i][x][y]なので何もしない。$O(1)$
E) $x$、$a$ を残す場合、すべての$x$について dp[i+3][x][a] <= dp[i][x][*]とする。$O(N)$
F) $a$, $b$ を残す場合、dp[i+3][a][b] <= dp[i][*][*]とする。$O(N)$
注意点
各$i$ごとに$O(1)$あるいは$O(N)$回の操作が必要になり、それを$O(N)$回繰り返すので、
全体としては$O(N^2)$となる。
dp[i][x][y]のように3次元配列にしてしまうと、TLE/MLEになってしまうので、In-placeでDPを更新する必要がある。
また、dp[i][x][*]は$y$を自由に選んだ時の最大値 max(dp[i][x][y]) とする。
$a$、$b$、$c$は順番を入れ替えて6パターン試しておく。