If $n \ge 4$ and $m \ge 4$, it’s impossible to satisfy condition A (the number of 1s contained in a square with even vertical and horizontal lengths is odd). For example, when a $2 \times 2$ square satisfies condition A, if you connect four such squares, the sum becomes even. That is, a $4 \times 4$ square cannot satisfy condition A.

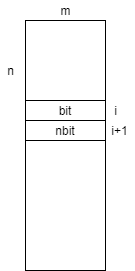
In all other cases, you can always satisfy condition A by performing operations several times. The minimum number of operations can be solved using DP. Let $dp_{i,bit}$ be the minimum number of operations when looking up to the $i$-th row and the $i$-th bit string is $bit$. The update formula is as follows. However, check that condition A is satisfied between $bit$ and $nbit$.
$$ \begin{aligned} dp_{i+1,nbit} \Leftarrow dp_{i, bit} + \sum_{j=0}^{m-1} ((nbit » j) \& 1) \oplus a_{i+1,j} \end{aligned} $$