It was a red difficulty problem. Reading the problem statement made it seem approachable, but it wasn’t that simple. First, I considered an $O(N^3)$ DP, then approached it by reducing the computational complexity based on that.
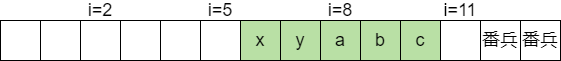
We look at $i = 2, 5, 8, 11, \dots$ at intervals of 3 characters.
Let dp[i][x][y] be the maximum score when we’ve examined up to the $i$-th position and the previous two characters are $x$ and $y$.
Let a = v[i], b = v[i+1], c = v[i+2] and consider different patterns.
Cases where score increases by +1. Consider which three to use for scoring.
A) When $a = b = c$, for all pairs $(x, y)$, dp[i+3][x][y] <= dp[x][y], so instead add +1 to the answer. $O(1)$
B) When $a = b = x$, for all $y$, dp[i+3][c][y] <= max(dp[i][a][*]) + 1. $O(N)$
C) When $a = x = y$, dp[i+3][b][c] <= dp[i][a][a] + 1. $O(N)$
Cases where score doesn’t increase by +1. Consider which two to keep.
D) Keep $x$ and $y$: dp[i+3][x][y] <= dp[i][x][y], so do nothing. $O(1)$
E) Keep $x$ and $a$: for all $x$, dp[i+3][x][a] <= dp[i][x][*]. $O(N)$
F) Keep $a$ and $b$: dp[i+3][a][b] <= dp[i][*][*]. $O(N)$
Important points
For each $i$, $O(1)$ or $O(N)$ operations are needed, and this is repeated $O(N)$ times, so overall it’s $O(N^2)$.
If we use a 3D array like dp[i][x][y], we’ll get TLE/MLE, so we need to update DP in-place.
Also, dp[i][x][*] represents the maximum value max(dp[i][x][y]) when $y$ is chosen freely.
Try 6 patterns by permuting $a$, $b$, $c$.